Question

Help help help help pls

Answer 1

The length of AB is approximately 6.07 m

Explanation:

The given dimensions of the triangle are;

The value of x = 7.7 m

The measure of angle, θ = 52°

The length of side AB = Required

The given triangle ΔABC is a right triangle, with the following sides;

AC = x = The hypotenuse (opposite to right angle) side

(Leg) AB = The opposite side to the reference angle, θ

(Leg) BC = The adjacent side to the reference angle, θ

By trigonometric ratio, we have;

`sin(\theta) = (Opposite \ leg \ length)/(Hypotenuse \ length) = (AB)/(x)`

Therefore;

`sin(52^(\circ)) = (AB)/(7.7)`

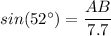
AB = 7.7 × sin(52°) ≈ 6.07

The length of AB ≈ 6.07 m.