Answer:
2. The ratio of the corresponding sides of ΔUTS and ΔUDE are not equal
3. ΔCBA ~ ΔHGF
4. ΔVUT ~ ΔVML
5. ΔTUV ~ ΔJKL
6. The ratio of all the corresponding sides and all the corresponding angles in triangles ΔSTU and ΔSCB are not equal
7. The ratio of the corresponding sides of triangles, ΔKLM and ΔKBC are not equal
Explanation:
2. The ratio of the corresponding sides of ΔUTS and ΔUDE are;
36/43, 16/39, and 16/40
We have;

∴ ΔUTS is not similar to ΔUDE, because the ration of the corresponding sides of both triangles are not equal
3. The interior angles of ΔCBA are;
∠A = 33°, ∠B = 88°, and ∠C = 59°
The interior angles of ΔHFG are;
∠H = 33°, ∠F = 59°, and ∠G = 88°
∴ ΔCBA ~ ΔHGF (ΔCBA is similar to ΔHGF) (Letters rearranged) by Angle-Angle, AA, similarity postulate
4. The measure of angle ∠LMV = 25° = The measure of angle ∠UTV Given
The measure of angle ∠MVL = ∠TVU by reflexive property
Therefore, ΔVUT ~ ΔVML (ΔVUT is similar to ΔVML) by Angle-Angle, AA, similarity postulate
5. The measure of angles ∠T and ∠U in triangle ΔTUV are equal to the measure of angles ∠J and ∠K in triangle ΔJKL
Therefore, ΔTUV ~ ΔJKL (ΔTUV is similar to ΔJKL) by Angle-Angle, AA, similarity postulate
6. In triangles ΔSTU and ΔSCB, we have;
The ∠TSU = ∠TSU by reflexive property
However, ∠SUT ≠ ∠SNC ≠ ∠STU
Therefore, ΔSTU is not similar to ΔSCB due to the triangles have one non equal angle
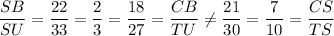
From which we get;
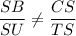
∴ ΔSTU is not similar to ΔSCB, because not all the ratio of the corresponding sides and angles are equal
7. The ratio of the corresponding sides of triangles, ΔKLM and ΔKBC are;
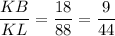
KM = KC + CM = 25 + 107 = 132

Therefore;

The ratio of the sides of triangles, ΔKLM and ΔKBC are;
Therefore ΔKLM and ΔKBC are not similar, because the ratio of the corresponding sides are not equal