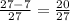Question

The numerator of a rational number is less thanits denominator by 7. If the new number becomes
`(3)/(2)` when the numerator is tripled and the denominator is increased by 13, find the original number.

Answer 1

Explanation:

If the numerator is 7 less than its denominator, than the original number in terms of x is

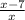`(x-7)/(x)`. If we triple the numerator, the expression to do this is 3(x - 7); if we increase the denominator, the expression to do this is x + 13. Putting that together along with the fact that after we do this manipulation the new number is 3/2:

`(3(x-7))/(x+13)=(3)/(2)` and distribute:

`(3x-21)/(x+13)=(3)/(2)` and cross multiply to get:

2(3x - 21) = 3(x + 13) and

6x - 42 = 3x + 39 and

3x = 81 so

x = 27. Subbing 27 for x into the original number:

`(27-7)/(27)=(20)/(27)`