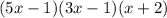Question

F(x)=15x³+22x²-15x+2
Write f(x) as a product of linear factors.

Answer 1

`(5x - 1)(3x - 1)(x + 2)`

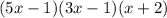
Explanation:

`(15 {x}^(3) + 22 {x}^(2) - 15x + 2)`

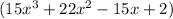
Apply Rational Root Theorem, our possible roots will be

plus or minus( 2/15, 2/5,2/3,2, 1/15,1/5,1/3,1).

I

I tried root -2 and it work so

If we apply synthetic dividon, we would be left with

`15 {x}^(2) - 8x + 1`

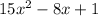
We can factor this regularly.

Apply AC method that a number

AC will multiply to 15 but add to -8.

The answer are -5 and -3 so we write this as

`15 {x}^(2) - 5x - 3x + 1`

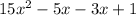
Factor by grouping

`(15x {}^(2) - 5x) - (3x + 1)`

`5x(3x - 1) - 1(3x - 1)`

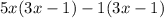
So our factor are

`(5x - 1)(3x - 1)(x + 2)`