Answer:
The midpoint of the segment with endpoints at the midpoints of s1 and s2 is (4,5).
Explanation:
Midpoint of a segment:
The coordinates of the midpoint of a segment are the mean of the coordinates of the endpoints of the segment.
Midpoint of s1:
Using the endpoints given in the exercise.
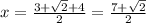
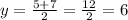
Thus:
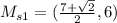
Midpoint of s2:
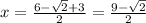
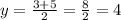
Thus:
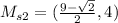
Find the midpoint of the segment with endpoints at the midpoints of s1 and s2.
Now the midpoint of the segment with endpoints
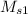 and
and
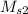 . So
. So
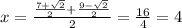
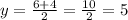
The midpoint of the segment with endpoints at the midpoints of s1 and s2 is (4,5).