Question

What are the first five terms of the recursive sequence

Answer 1

Answer: Choice D

9, 30, 93, 282, 849

============================================================

Step-by-step explanation:

The notation
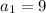`a_1 = 9` tells us that the first term is 9

The notation
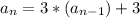`a_n = 3*(a_(n-1))+3` says that we multiply the (n-1)st term by 3, then add on 3 to get the nth term
`a_n`

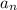
So if we wanted the second term for instance, then we'd say

`a_n = 3*(a_(n-1))+3\\\\a_2 = 3*(a_(2-1))+3\\\\a_2 = 3*(a_(1))+3\\\\a_2 = 3*(9)+3\\\\a_2 = 27+3\\\\a_2 = 30\\\\`

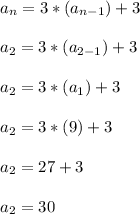
If we want the third term, then,

`a_n = 3*(a_(n-1))+3\\\\a_3 = 3*(a_(3-1))+3\\\\a_3 = 3*(a_(2))+3\\\\a_3 = 3*(30)+3\\\\a_3 = 90+3\\\\a_3 = 93\\\\`

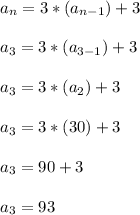
and so on.

The terms so far are: 9, 30, 93

You should find the fourth and fifth terms are 282 and 849 respectively if you keep this pattern going.

Therefore, the answer is choice D