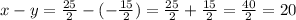Question

X^2 - y^2 = 100

x + y = 5
The solution to the given system of equations is
(x, y). What is the value of x - y?

Answer 1

20

Explanation:

Let's start by rewriting the second equation in terms of "x":

`x+y=5`

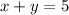
Subtract y from both sides:

`x=5-y`

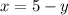
Now, substitute "5-y" for "x" in the first equation:

`(5-y)^2-y^2=100`

Note that:

`(a-b)^2=a^2-2ab+b^2`

`25-10y+y^2-y^2=100`

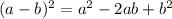
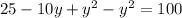
Cancel out like terms:

`25-10y=100`

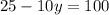
Subtract 25 from both sides:

`-10y=75`

Divide both sides by -10

`y=(75)/(-10)=(15)/(-2)=-(15)/(2)`

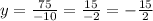
Now, substitute this value back into either of the equations to solve for x.

`x+y=5\\x-(15)/(2)=5\\`

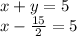
Add 15/2 to both sides:

`x=5+(15)/(2)\\x=(10)/(2)+(15)/(2)\\x=(25)/(2)`

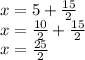
Now, find the difference:

`x-y=(25)/(2)-(-(15)/(2))=(25)/(2)+(15)/(2)=(40)/(2)=20`