Given:
Leila is arranging 11 cans of food in a row on a shelf. She has 4 cans of corn, 1 can of peas, and 6 cans of beets.
To find:
The distinct orders can the cans be arranged if two cans of the same food are considered identical.
Solution:
Total number of cans = 11
Cans of corn = 4
Cans of Peas = 1
Cans of beets = 6
We need to find divide total possible arrangements (11!) by the repeating arrangements (1!, 4!, 6!) to find the distinct orders can the cans be arranged if two cans of the same food are considered identical.
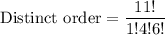
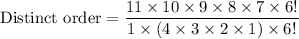
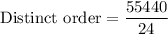
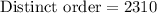
Therefore, the total number of distinct orders is 2310.