Question

The ejection seat has an acceleration of 8gees (8xgravity or ~80m/s/s). He has a mass of 70kg. The total force on him from the chair/rocket would be.

A) (80m/s/s)(70kg)=5600N
B) (80m/s/s)(70kg)=5600N + Fg = 5600N+(70kg)(9.8N/kg)~5600N+700N=6300N
C) (80m/s/s)(70kg)=5600N - Fg = 5600N+(70kg)(9.8N/kg)~5600N-700N=4900N
D) I need the time

Answer 1

B) (80m/s/s)(70kg)=5600N + Fg = 5600N+(70kg)(9.8N/kg)~5600N+700N=6300N

Step-by-step explanation:

The total force by the chair is given by the following formula:

`F = m(g+a)`

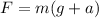
where,

F = Force = ?

m = mass of person = 70 kg

g = value of acceleration dueto gravity = 9.81 m/s²

a = acceleration of ejection seat = 8g = 80 m/s²

Therefore,

`F = mg+ma \\F = (70\ kg)(9.8\ m/s^2)+(70\ kg)(80\ m/s^2)\\F = 6300 N`

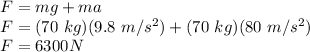
Therefore, the correct option is:

B) (80m/s/s)(70kg)=5600N + Fg = 5600N+(70kg (9.8N/kg)~5600N+700N=6300N