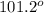Question

in triangle abc |BC|=4.12cm ,|AC|=6.82cm and angle BCA is 42.5 . Calculate|AB| . and angle bac and angle abc​

Answer 1

i. |AB| = 4.70 cm

ii. BAC =
`36.3^(o)`

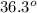
iii. ABC =
`101.2^(o)`

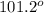
Step-by-step explanation:

i Let |AB| be represented by c, |AC| by b and |BC| by a. Since the question would give an included angle triangle, we first apply cosine rule.

`c^(2)` =
`a^(2)` +
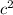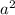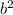`b^(2)` - 2ab Cos C

=
`(4.12)^(2)` +
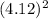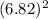`(6.82)^(2)` - 2(4.12*6.82) Cos
`42.5^(o)`

= 16.9744 + 46.5124 - 56.1968*0.7373

= 63.4868 - 41.4340

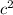`c^(2)` = 22.0528

c =
`√(22.0528)`

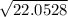
= 4.6960

c = 4.70 cm

Thus |AB| = 4.70 cm

ii. Applying the sine rule;

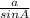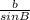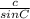
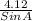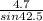
`(a)/(sin A)` =
`(b)/(sin B)` =
`(c)/(sin C)`

`(4.12)/(Sin A)` =
`(4.7)/(sin 42.5)`

sin A =
`(4.12*sin 42.5)/(4.7)`

= 0.5922

A =
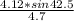
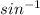`sin^(-1)` 0.5922

= 36.3

BAC =
`36.3^(o)`

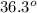
But,

iii. BCA + BAC + ABC =
`180^(o)`

`42.5^(o)` +
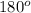
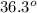`36.3^(o)` + ABC =
`180^(o)`

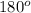
ABC =
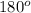`180^(o)` - 78.8

= 101.2

ABC =
`101.2^(o)`