Question

Calculus 2. Please help

Answer 1

`\displaystyle \int\limits^1_0 {(1)/(xe^(x^2))} \, dx = \infty`

General Formulas and Concepts:

Algebra I

• Exponential Rule [Rewrite]:
  `\displaystyle b^(-m) = (1)/(b^m)`

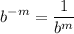
Calculus

Limits

• Right-Side Limit:
  `\displaystyle \lim_(x \to c^+) f(x)`

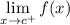
Limit Rule [Variable Direct Substitution]:
`\displaystyle \lim_(x \to c) x = c`

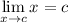
Derivatives

Derivative Notation

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Integrals

• Definite Integrals

Integration Constant C

Integration Rule [Fundamental Theorem of Calculus 1]:
`\displaystyle \int\limits^b_a {f(x)} \, dx = F(b) - F(a)`

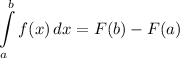
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

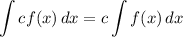
U-Substitution

U-Solve

Improper Integrals

Exponential Integral Function:
`\displaystyle \int {(e^x)/(x)} \, dx = Ei(x) + C`

Explanation:

Step 1: Define

Identify

`\displaystyle \int\limits^1_0 {(1)/(xe^(x^2)) \, dx`

Step 2: Integrate Pt. 1

1. [Integral] Rewrite [Exponential Rule - Rewrite]:
   `\displaystyle \int\limits^1_0 {(1)/(xe^(x^2)) \, dx = \int\limits^1_0 {(e^(-x^2))/(x) \, dx`
2. [Integral] Rewrite [Improper Integral]:
   `\displaystyle \int\limits^1_0 {(1)/(xe^(x^2)) \, dx = \lim_(a \to 0^+) \int\limits^1_a {(e^(-x^2))/(x) \, dx`

Step 3: Integrate Pt. 2

Identify variables for u-substitution.

1. Set:
   `\displaystyle u = -x^2`
2. Differentiate [Basic Power Rule]:
   `\displaystyle (du)/(dx) = -2x`
3. [Derivative] Rewrite:
   `\displaystyle du = -2x \ dx`

Rewrite u-substitution to format u-solve.

1. Rewrite du:
   `\displaystyle dx = (-1)/(2x) \ dx`

Step 4: Integrate Pt. 3

1. [Integral] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle \int\limits^1_0 {(1)/(xe^(x^2)) \, dx = \lim_(a \to 0^+) -\int\limits^1_a {-(e^(-x^2))/(x) \, dx`
2. [Integral] Substitute in variables:
   `\displaystyle \int\limits^1_0 {(1)/(xe^(x^2)) \, dx = \lim_(a \to 0^+) -\int\limits^1_a {(e^(u))/(-2u) \, du`
3. [Integral] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle \int\limits^1_0 {(1)/(xe^(x^2)) \, dx = \lim_(a \to 0^+) (1)/(2)\int\limits^1_a {(e^(u))/(u) \, du`
4. [Integral] Substitute [Exponential Integral Function]:
   `\displaystyle \int\limits^1_0 {(1)/(xe^(x^2)) \, dx = \lim_(a \to 0^+) (1)/(2)[Ei(u)] \bigg| \limits^1_a`
5. Back-Substitute:
   `\displaystyle \int\limits^1_0 {(1)/(xe^(x^2)) \, dx = \lim_(a \to 0^+) (1)/(2)[Ei(-x^2)] \bigg| \limits^1_a`
6. Evaluate [Integration Rule - FTC 1]:
   `\displaystyle \int\limits^1_0 {(1)/(xe^(x^2)) \, dx = \lim_(a \to 0^+) (1)/(2)[Ei(-1) - Ei(a)]`
7. Simplify:
   `\displaystyle \int\limits^1_0 {(1)/(xe^(x^2)) \, dx = \lim_(a \to 0^+) (Ei(-1) - Ei(a))/(2)`
8. Evaluate limit [Limit Rule - Variable Direct Substitution]:
   `\displaystyle \int\limits^1_0 {(1)/(xe^(x^2)) \, dx = \infty`

∴
`\displaystyle \int\limits^1_0 {(1)/(xe^(x^2)) \, dx` diverges.

Topic: Multivariable Calculus