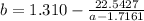Question

How do I solve for a and b using the Van Der Waals equation using only the given values: P= 1 atm, V= 1.310 L, and T= 160 K

Answer 1

`a = (24.79078- 1.7161b)/(1.310 - b)`

`b = 1.310 - (22.5427)/(a - 1.7161)`

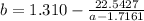
Step-by-step explanation:

Given

`P = 1\ atm`

`V = 1.310\ L`

`T =160\ K`

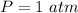
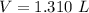
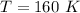
Required

Solve for a and b

Van Der Waals equation is:

`P = (RT)/(V - b) - (a)/(V^2)`

Substitute values for P, V and T, we have:

`1 = (R*160)/(1.310 - b) - (a)/(1.310^2)`

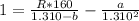
R is a constant and the value is:

`R = 0.0821`

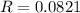
So, the equation becomes:

`1 = (0.0821*160)/(1.310 - b) - (a)/(1.310^2)`

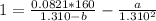
Simplify the expression

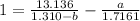`1 = (13.136)/(1.310 - b) - (a)/(1.7161)` ----- (a)

Solving for (a):

`1 + (13.136)/(1.310 - b) = (a)/(1.7161)`

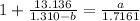
Multiply both sides by 1.7161

`a = [1 + (13.136)/(1.310 - b)] * 1.7161`

Take LCM

`a = [(1.310 - b+13.136)/(1.310 - b)] * 1.7161`

Evaluate like terms

`a = [(14.446- b)/(1.310 - b)] * 1.7161`

Open bracket

`a = [(24.79078- 1.7161b)/(1.310 - b)`

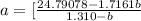
Solving for (b), we have:

`1 + (13.136)/(1.310 - b) = (a)/(1.7161)`

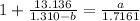
Subtract 1 from both sides

`(13.136)/(1.310 - b) = (a)/(1.7161)-1`

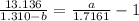
Take LCM

`(13.136)/(1.310 - b) = (a-1.7161)/(1.7161)`

Inverse both sides

`(1.310 - b)/(13.136) = (1.7161)/(a - 1.7161)`

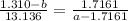
Multiply both sides by 13.136

`1.310 - b = 13.136 * (1.7161)/(a - 1.7161)`

`1.310 - b = (22.5427)/(a - 1.7161)`

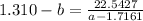
Collect like terms

`b = 1.310 - (22.5427)/(a - 1.7161)`