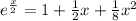Explanation:
Starting out with the Taylor series,
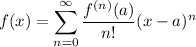
where
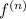 is the nth derivative of f(x) and if we set a = 0, we get the special case of the Taylor series called the Maclaurin series:
is the nth derivative of f(x) and if we set a = 0, we get the special case of the Taylor series called the Maclaurin series:
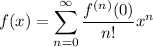
Expanding this series up to the 1st 3 terms at a = 0,
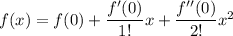
Let's find the derivatives of
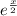 :
:
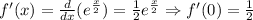
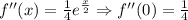
We can now write the Maclaurin series for
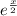 as
as