Answer:
The general limit exists at x = 9 and is equal to 300.
Explanation:
We want to find the general limit of the function:
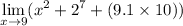
By definition, a general limit exists at a point if the two one-sided limits exist and are equivalent to each other.
So, let's find each one-sided limit: the left-hand side and the right-hand side.
The left-hand limit is given by:
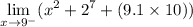
Since the given function is a polynomial, we can use direct substitution. This yields:
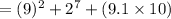
Evaluate:
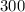
Therefore:
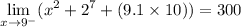
The right-hand limit is given by:
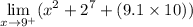
Again, since the function is a polynomial, we can use direct substitution. This yields:
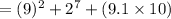
Evaluate:
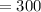
Therefore:
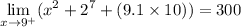
Thus, we can see that:
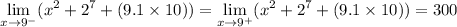
Since the two-sided limits exist and are equivalent, the general limit of the function does exist at x = 9 and is equal to 300.