Answer:
m∠CAB = 66°
m∠CAD = 24°
Explanation:
m∠CAB
The given parameters are;
The measure of arc m
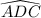 = 228°
= 228°
The diameter of the given circle =

The tangent to the circle =
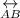
The measure of m∠CAB and m∠CAD = Required
By the tangent and chord circle theorem, we have;
m∠CAB = (1/2) × m
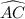
However, we have;
m
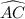 + m
+ m
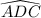 = 360° the sum of angles at the center of a circle is 360°
= 360° the sum of angles at the center of a circle is 360°
∴ m
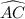 = 360° - m
= 360° - m
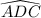
Which gives;
m
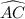 = 360° - 228° = 132°
= 360° - 228° = 132°
m
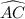 = 132°
= 132°
Therefore;
m∠CAB = (1/2) × 132° = 66°
m∠CAB = 66°
m∠CAD
Given that
 is the diameter of the given circle, we have
is the diameter of the given circle, we have
The tangent,
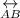 , is perpendicular to the radius of the circle, and therefore
, is perpendicular to the radius of the circle, and therefore
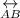 is also perpendicular to the diameter of the circle
is also perpendicular to the diameter of the circle
∴ m∠DAB = 90° which is the measure of the angle formed by two perpendicular lines
By angle addition property, we have;
m∠DAB = m∠CAB + m∠CAD
∴ m∠CAD = m∠DAB - m∠CAB
By substitution, we have;
m∠CAD = 90° - 66° = 24°
m∠CAD = 24°