Given:
The function is:
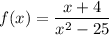
To find:
The values that are NOT in the domain of the given function.
Solution:
We have,
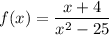
This function is a rational function and it is defined for all real values of x except the values for which the denominator is equal to 0.
Equate the denominator and 0.
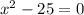
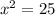
Taking square root on both sides, we get
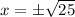

So, the values
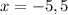 are not in the domain of the given function.
are not in the domain of the given function.
Therefore, the correct option is D.