Question

Find the fifth term and the nth term of the geometric sequence whose initial term, a, and common ratio, r, are given.

a = 8; r = -5

Answer 1

`a_n = 8(-5)^(n-1)`

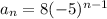
The fifth term of the sequence is 5000.

Explanation:

Geometric sequence:

In a geometric sequence, the quotient between consecutive terms is always the same, called common ratio. The nth term of a geometric sequence is:

`a_n = a_1(r)^(n-1)`

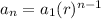
a = 8; r = -5

Thus:

`a_n = a_1(r)^(n-1)`

`a_n = 8(-5)^(n-1)`

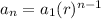
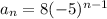
Fifth term:

This is
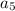`a_5`. So

`a_5 = 8(-5)^(5-1) = 5000`

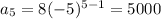
The fifth term of the sequence is 5000.