Given:
A fair die is rolled.
It pays off $10 for 6, $7 for a 5, $4 for a 4 and no payoff otherwise.
To find:
The expected winning for this game.
Solution:
If a die is rolled then the possible outcomes are 1, 2, 3, 4, 5, 6.
The probability of getting a 6 is:
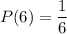
The probability of getting a 5 is:
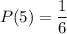
The probability of getting a 4 is:

The probability of getting other numbers (1,2,3) is:
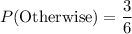
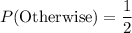
We need to find the sum of product of payoff and their corresponding probabilities to find the expected winning for this game.

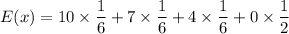
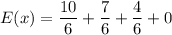
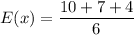
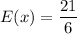

Therefore, the expected winnings for this game are $3.50.