Answer:
The area of the rectangle is increasing at a rate of 84 square centimeters per second.
Explanation:
The area for a rectangle is given by the formula:
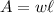
Where w is the width and l is the length.
We are given that the length of the rectangle is increasing at a rate of 6 cm/s and that the width is increasing at a rate of 5 cm/s. In other words, dl/dt = 6 and dw/dt = 5.
First, differentiate the equation with respect to t, where w and l are both functions of t:
![\displaystyle (dA)/(dt)=(d)/(dt)\left[w\ell]](https://img.qammunity.org/2022/formulas/mathematics/college/yq6gcdzar7qn01j2jubgk5c415bmstjw1d.png)
By the Product Rule:
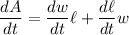
Since we know that dl/dt = 6 and that dw/dt = 5:
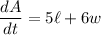
We want to find the rate at which the area is increasing when the length is 12 cm and the width is 4 cm. Substitute:

The area of the rectangle is increasing at a rate of 84 square centimeters per second.