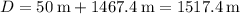1517.4 m
Step-by-step Step-by-step explanation:
Since the projectile broke up at the peak of its flight, it already traveled half its initial range so we can find its initial launch velocity
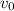 from the equation
from the equation
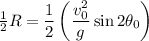
where
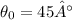 and
and
 so we will get
so we will get
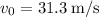 . Next, we can use the equation
. Next, we can use the equation
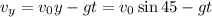
and since
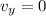 at its peak, we get t = 22.1 s. Let's set this aside for a moment and we'll use it later.
at its peak, we get t = 22.1 s. Let's set this aside for a moment and we'll use it later.
At the top of its peak, we can use the conservation law of linear momentum. Let M be the mass if of the original projectile,
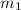 be the mass of the larger fragment (2 kg) and
be the mass of the larger fragment (2 kg) and
 be the mass of the smaller fragment (1 kg). We can write the conservation law as
be the mass of the smaller fragment (1 kg). We can write the conservation law as
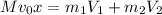
where
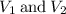 are the velocities of the fragments immediately after the break up. But we also know that
are the velocities of the fragments immediately after the break up. But we also know that
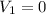 so the velocity of
so the velocity of
 can be calculated from the conservation law as
can be calculated from the conservation law as
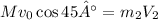
or
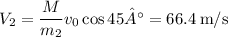
Now we can calculate the horizontal distance the smaller fragment traveled after the break up. Recall that the amount of time for it to go up is also the amount of time to get down so the horizontal distance x is
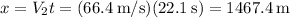
Therefore, the total distance traveled from the launch point is