Answer:
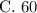
Explanation:
Question from image:
"The digits 1, 2, 3, 4, and 5 can be formed to arrange 120 different numbers. How many of these numbers will have the digits 1 and 2 in increasing order? For example, 14352 and 51234 are two such numbers."
Let's start by taking a look with the number 1. There are four possible places 1 could be, because there needs to be space for the 2 after it.
Checkmarks mark where the 1 can be, the x marks where it cannot be.

Let's start with the first position:
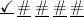
There are four places the 2 can be. For each of these four places, we can arrange the remaining 3 digits in
 ways. Therefore, there are
ways. Therefore, there are
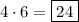 possible numbers when 1 is the first digit of the number.
possible numbers when 1 is the first digit of the number.
Continue this process with the remaining possible positions for 1.
Second position:
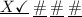
There are three places the 2 can be, since the 2 must be behind the 1. For each of these three places, the remaining 3 digits can be arranged in
 ways. Therefore, there are
ways. Therefore, there are
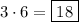 possible numbers when 1 is the second digit of the number.
possible numbers when 1 is the second digit of the number.
The pattern continues. Next there will be 2 places to place the 2. For each of these, there are
 ways to rearrange the remaining 3 digits for a total of
ways to rearrange the remaining 3 digits for a total of
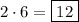 possible numbers when 1 is the third digit of the number.
possible numbers when 1 is the third digit of the number.
Lastly, when 1 is the fourth digit of the number, there is only 1 place the 2 can be. For this one place, there are still
 ways to rearrange the remaining three numbers. Therefore, there are
ways to rearrange the remaining three numbers. Therefore, there are
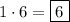 possible numbers when 1 is the fourth digit of the number.
possible numbers when 1 is the fourth digit of the number.
Thus, there are
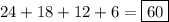 numbers that will have the digits 1 and 2 in increasing order, from a set of 120 five-digit numbers created by the digits 1 through 5, where no digit may be repeated.
numbers that will have the digits 1 and 2 in increasing order, from a set of 120 five-digit numbers created by the digits 1 through 5, where no digit may be repeated.