Question

NEED HELP WITH THIS PLEASE. Just show me how please.

Answer 1

Given:

The quadratic equation is:

`-5x^2-3x-2=0`

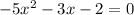
To find:

The discriminant of the given equation and the number of real solutions.

Solution:

If a quadratic equation is
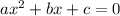`ax^2+bx+c=0`, then the value of discriminant is:

`D=b^2-4ac`

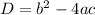
If D<0, then the quadratic equation has no real roots or two imaginary roots.

If D=0, then the quadratic equation has two equal real roots.

If D>0, then the quadratic equation has two distinct real roots.

We have,

`-5x^2-3x-2=0`

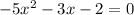
Here,
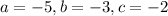`a=-5,b=-3,c=-2`. So, the discriminant of the given equation is:

`D=(-3)^2-4(-5)(-2)`

`D=9-40`

`D=-31`

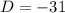
Since D<0, therefore the number of real solutions is 0.

Hence, the value of the discriminant is -31 and the number of real solutions is 0.