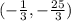Question

What is the vertex of the parabola with the equation y
3x2 + 2x – 8?

Answer 1

Explanation:

If you're tasked to do this mathematically, you have to complete the square to get it into vertex, or work, form. Do that by first setting the equation equal to 0 then moving over the constant:

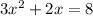`3x^2+2x=8` Next you have to have a +1 as the leading coefficient, and ours is a 3, so we factor it out:

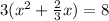`3(x^2+(2)/(3)x)=8`. Now take half the linear term, square it, and add it in to both sides. Our linear term is 2/3. Half of 2/3 is 2/6 which reduces to 1/3. Squaring 1/3 gives us 1/9, so that's what we add in.

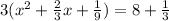`3(x^2+(2)/(3)x+(1)/(9))=8+(1)/(3)` to the right of the equals sign we added in 3*1/9 which is 3/9, which reduces to 1/3. Now we clean up both sides. The right side is easy; the left side, not so much. The reason we do this (complete the square) is to get a perfect square binomial on the left. When we re-write the left side into that perfect square binomial, we get

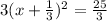`3(x+(1)/(3))^2=(25)/(3)` Now we move the constant back over and set the parabola back equal to y:

`y=3(x+(1)/(3))^2-(25)/(3)` which shows us that the vertex is

`(-(1)/(3),-(25)/(3))`