Question

Find the investment value when compounded anually.
P = $120,000, r= 5.3%, t = 8 yr​

Answer 1

Given:

`P=\$120,000`

`r=5.3\%`

`t=8\text{ years}`

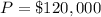
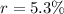
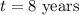
To find:

The value of the investment when the interest is compounded annually.

Solution:

The formula for amount is:

`A=P\left(1+(r)/(n)\right)^(nt)`

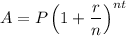
Where, P is the principal, r is the rate of interest in decimal, n is the number of time interest compounded in an years, and t is the number of years.

The interest is compounded annually. So,
`n=1`.

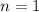Substituting
`P=120000, r=0.053, n=1, t=8` in the above formula, we get

`A=120000\left(1+(0.053)/(1)\right)^(1(8))`

`A=120000\left(1.053\right)^(8)`

`A=181387.85936`

`A\approx 181387.86`

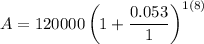
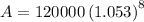
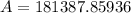
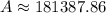
Therefore, the value of the investment after 8 years is $181,387.86.