Explanation:
"must be used first" is a very hard phrasing. multiplication is commutative.
and I am not sure that the problem is stated correctly.
I read here
(i×y²) to the power of 1/3.
i is the imaginary constant sqrt(-1) ?
exponents brought themselves to the power of something else multiply.
e.g.
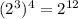
exponents in multimedia expressions of the same base simply add up.
e.g.
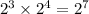
a negative exponent means that the expression with the same positive exponent is just at the bottom of a division.
e.g.
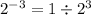
and a fraction as exponent specifies a root to be taken.
e.g
![{2}^(1 / 3) = \sqrt[3]{2}](https://img.qammunity.org/2022/formulas/mathematics/high-school/tyc1ak17ngod4hi4v586mnqgi78on34sh4.png)
so, I would do all the exponent multiplications to simplify the expression.
![\sqrt[3]{i * {y}^(2) } = ({i * {y}^(2) })^(1 / 3) =](https://img.qammunity.org/2022/formulas/mathematics/high-school/1oopq8yr4rwxvtppba45pp8it2f9gje9z8.png)
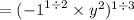
1/2 × 1/3 = 1/6
2 × 1/3 = 2/3
![= { - 1}^(1 / 6) * {y}^(2 / 3) = \sqrt[6]{ - 1} * \sqrt[3]{ {y}^(2) }](https://img.qammunity.org/2022/formulas/mathematics/high-school/w962sb93s7ievzy175iz3s6eeqidu2twyt.png)
so, as we can see, we can move freely from multiplying the fraction exponents to converting them into root expressions and vice versa.