Answer:
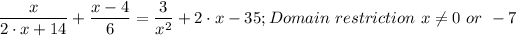
Explanation:
The given rational equation is presented here as follows;
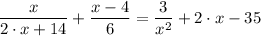
A domain restriction are the limits to the ranges of input values (x-values) of a function
The three main types of domain restrictions are the reciprocal function, the log function, and the root function
The form of restriction in the given rational are reciprocal form, which are;
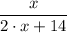 , and
, and
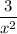 , from which the function is undefined when;
, from which the function is undefined when;
2·x + 14 = 0, therefore when x = -7, or x² = 0, when x = 0
Therefore, the domain restrictions are that the function is defines for all x, except x = -7 and x = 0
The domain restrictions are x ≠ -7 and x ≠ 0.