Answer:
n ∝ (1/l) (√F/m)
Explanation:
Since frequency, n of vibration of a stretched string is a function of its tension F, the length l and the mass per unit length m, and has dimensions [T]⁻¹ where T = time, its dimension must be equal to that of the combination of F, L and m
Since n = f(F,L,m)
n = kFᵃLᵇmˣ
dimension of n = (dimension of F)ᵃ × (dimension of L)ᵇ × (dimension of m)ˣ
Since n = frequency, dimension of n = [T]⁻¹
F = Force, dimension of F = [M][L][T]⁻²
Also, L = length, dimension of L = [L] and
m = mass per unit length, dimension of m = [M][L]⁻¹
So, n = FᵃLᵇmˣ
[T]⁻¹ = ([M][L][T]⁻²)ᵃ( [L] )ᵇ([M][L]⁻¹)ˣ
[T]⁻¹ = ([M]ᵃ[L]ᵃ[T]⁻²ᵃ[L]ᵇ([M]ˣ[L]⁻ˣ
[M]⁰[L]⁰[T]⁻¹ = ([M]ᵃ ⁺ˣ)([L]ᵃ ⁺ ᵇ ⁻ˣ)([T]⁻²ᵃ)
equating the exponents on both sides, we have
a + x = 0 (1 )⇒ x = -a
a + b - x = 0 (2) ⇒
-2a = -1 (3) ⇒ a = 1/2
Substituting x into 2, we have
a + b -(-a) = 0
a + b + a = 0
2a + b = 0
b = -2a
b = -2 (1/2)
b = -1
x = -a = -1/2
So, substituting the variables into n, we have
n = kFᵃLᵇmˣ
n = kFᵃLᵇmˣ
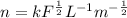
n = k/l(√F/m)
n ∝ (1/l) (√F/m)