Answer:
The measure of the first angle is 50°.
Explanation:
Let the three angles be a, b, and c.
The measure of the first angle is twice the measure of the second angle. In other words:

The measure of the third angle is 80° more than the measure of the second angle. In other words:
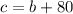
And since the interior angles of a triangle must equal 180°:
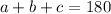
Substitute a and c:
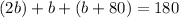
Combine like terms:
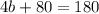
Subtract 80 from both sides:
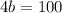
And divide both sides by four:
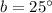
So, the measure of the second angle is 25°.
Since the measure of the first is twice the second, the measure of the first angle is 50°.
(And since the measure of the third is 80° than the second, the measure of the third angle is 105°.)