Question

Lauren pushed a crate of mass 28.9 kg a distance of 2.7 meters along a horizontal surface. On that part of the surface, the crate could slide with negligible friction. Lauren exerted a constant force of 121 newtons for 2.7 meters. The crate then slid down an inclined plane of height 1.8 meters, also with negligible friction. As the crate slid down the plane, the only significant forces on it were the normal force from the plane and gravity (with g = 9.81 meters per second squared). At the bottom of the incline, the crate began sliding along a horizontal surface with ordinary kinetic friction. The coefficient of friction between this surface and the crate was 0.41. This surface ended at a vertical wall after a distance of d2 = 5.2 meters but the crate did not slide that far. Attached to the vertical wall was a long ideal spring with length dy = 3.4 meters and a spring constant of 154 newtons per meter.

Required:
Calculate the distance that the crate compressed the spring before coming to rest.

Answer 1

3.034 m

Step-by-step explanation:

From the law of conservation of energy, the energy at the top of the incline equals the energy at the bottom of the incline since at the top of the incline, the horizontal surface is frictionless and along the incline there is no friction.

The work done in moving the crate a distance, d = 2.7 m with a force of F = 121 N to the top of the incline is W = Fd = 121 N × 2.7 m = 326.7 J.

From work-kinetic energy principles, this work W = kinetic energy of the crate at the top of the incline, K₁.

Now, the total mechanical energy at the top of the incline, E equals the total mechanical energy at the bottom of the incline E' since there is no friction along the incline.

So, E = E'

U₁ + K₁ = U₂ + K₂ where U₁ = potential energy of crate at top of incline = mgh where m = mass of crate = 28.9 kg, g = acceleration due to gravity = 9.8 m/s², h = height of incline = 1.8 m, K₁ = kinetic energy of crate at top of incline = 326.7 J, U₂ = potential energy of crate at bottom of incline = 0 J(since it is at an elevation h = 0) and K₂ = kinetic energy of crate at bottom of incline

So, substituting the values of the variables into the equation, we have

U₁ + K₁ = U₂ + K₂

mgh + K₁ = U₂ + K₂

28.9 kg × 9.8 m/s² × 1.8 m + 326.7 J = 0 J + K₂

509.796 J + 326.7 J = K₂

K₂ = 836.496 J

K₂ ≅ 836.5 J

Now since the vertical wall is a distance d2 away and the long ideal spring has a length dy = 3.4 m, let x be the compression of the spring. So, the distance moved by the crate is thus D = d2 - dy - x.

Now, the change in kinetic energy of the crate ΔK equals the work done by friction and that done by the spring W.

So ΔK = -W (from work-kinetic energy principles)

Let W' = work done by friction = μmgD where μ = coefficient of kinetic friction between surface and crate = 0.41, m = mass of crate = 28.9 kg, g = acceleration due to gravity = 9.8 m/s² and D = distance moved by crate = D = d2 - dy - x = 5.2 m - 3.4 m - x = 1.8 - x

So, W' = μmgD

W' = 0.41 × 28.9 kg × 9.8 m/s² (1.8 - x)

W' = 116.12(1.8 - x)

W' = 2090.16 - 116.12x

The work done by the spring W" = 1/2k(x₀² - x²) where k = spring constant = 154 N/m, x₀ = initial spring length = dy = 3.4 m and x = final spring compression.

So, W" = 1/2k(x₀² - x²)

W" = 1/2 × 154 N/m[(3.4 m)² - x²]

W" = 77 N/m[11.56 m² - x²]

W" = 890.12 - 77x²

So, W = W' + W"

W = 2090.16 - 116.12x + 890.12 - 77x²

W = 2980.28 - 116.12x - 77x²

Since the crate stops, final kinetic energy K₃ = 0. So, ΔK = K₃ - K₂ = 0 - 836.5 J = -836.5 J

Also, ΔK = -W

-836.5 = -(2980.28 - 116.12x - 77x²)

836.5 = 2980.28 - 116.12x - 77x²

77x² + 116.12 -2980.28 + 836.5 = 0

77x² + 116.12x -2143.78 = 0

dividing through by 77, we have

x² + 1.508x -27.841 = 0

Using the quadratic formula to find x, we have

`x = \frac{-1.508 +/-\sqrt{1.508^(2) - 4 X 1 X (-27.841)} }{2 X 1.508} \\x = (-1.508 +/-√(2.274064 + 111.364) )/(3.016) \\x = (-1.508 +/-√(113.638064) )/(3.016) \\x = (-1.508 +/- 10.66)/(3.016) \\x = (-1.508 - 10.66)/(3.016) or x = (-1.508 + 10.66)/(3.016) \\x = (-12.168)/(3.016) or x = (9.152)/(3.016) \\x = -4.03 or 3.034`

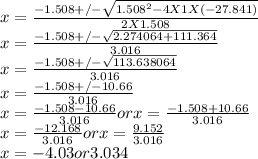
x = -4.03 or 3.034

Since the compression of the spring is positive, we choose x = 3.034

So, the crate compresses the spring 3.034 m