Answer:
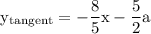
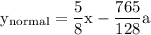
Explanation:
we are given a equation of parabola and we want to find the equation of tangent and normal lines of the Parabola
finding the tangent line
equation of a line given by:
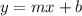
where:
- m is the slope
- b is the y-intercept
to find m take derivative In both sides of the equation of parabola
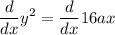
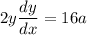
divide both sides by 2y:
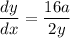
substitute the given value of y:

simplify:

therefore
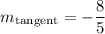
now we need to figure out the x coordinate to do so we can use the Parabola equation
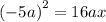
simplify:
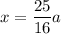
we'll use point-slope form of linear equation to get the equation and to get so substitute what we got

simplify which yields:

finding the equation of the normal line
normal line has negative reciprocal slope of tangent line therefore
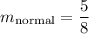
once again we'll use point-slope form of linear equation to get the equation and to get so substitute what we got
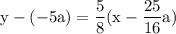
simplify which yields:
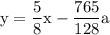
and we're done!
( please note that "a" can't be specified and for any value of "a" the equations fulfill the conditions)