Answer:
Explanation:
Smaller Canister:
Height, h = 12cm
Diameter = 9cm
Radius, r = 4.5 cm
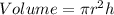
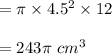
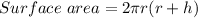
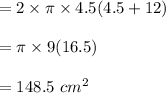
Larger Canister:
Measures double the smaller canister, that is
height, H = 24 cm
Diameter = 18cm
Radius, R = 9cm
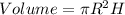
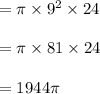
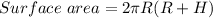
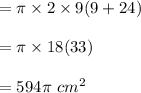
Comparing results :
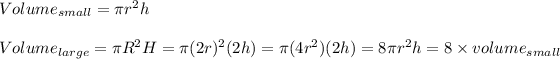
Therefore, volume of larger canister is 8 times the volume of smaller canister.
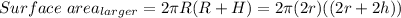

Therefore, surface area of larger canister is 4 times the surface area of smaller canister.