 Diameter of base of a cylinder = 20 cm.
Diameter of base of a cylinder = 20 cm.
 Height of cylinder = 5cm.
Height of cylinder = 5cm.


 Volume of Cylinder.
Volume of Cylinder.

To find volume of Cylinder first we should know radius of Cylinder. We can get radius by diameter using this formula:-
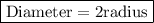



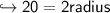

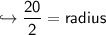

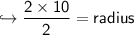

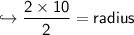

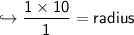

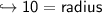

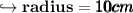

Now Finally Let's find volume of Cylinder.
we know:-
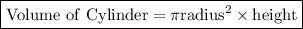

So:-
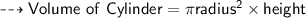





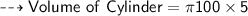

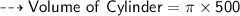





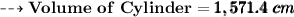
KNOW MORE:-
