Question

Consultant plans a survey to determine what % of the patients in a particular hospital were satisfied with the care they received after a major treatment. How many such patients should be surveyed so the margin of error for a 90% confidence interval is within .05? Suppose it is known from a past survey that such a % may be about 80%.

Answer 1

Required margin of error = 0.05

Estimated population proportion p = 0.8

Significance level = 0.10

The
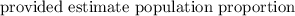`\text{provided estimate population proportion}` p is 0.8

The significance level, α = 0.1 is
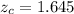`z_c=1.645`, which is obtained by looking into a standard normal probability table.

The number of patients surveyed to estimate the population proportion p within the required margin of error :

`$n \geq p(1-p)\left((z_c)/(E)\right)^2$`

`$=0.8* (1-0.8)\left((1.64)/(0.05)\right)^2$`

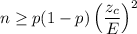
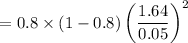
= 173.15

Therefore, the number of patients surveyed to satisfy the condition is n ≥ 173.15 and it must be an integer number.

Thus we conclude that the number of patients surveyed so the margin of error of 90% confidence interval is within 0.05 are n= 174.