Question

A 20-g bullet moving at 1000 m/s is fired through a 1kg block of wood emerging at a speed of 100m/s.what is the change in kinetic energy of the bullet

Answer 1

D. 0.16 KJ

Step-by-step explanation:

Given the following data;

Initial velocity, U = 1000 m/s

Mass of bullet, M1 = 20 g to kilograms = 20/1000 = 0.02 kg

Mass of block, M2 = 1 kg

Final velocity, V = 100 m/s

To find the change in kinetic energy;

First of all, we would determine the velocity after the collision by applying the law of conservation of momentum.

`M_(1)U - M_(1)V = M_(2)V_(f)`

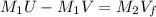
Substituting into the above formula, we have;

`0.02*1000 - 0.02*100 = 1*V_(f)`

`20 - 2 = V_(f)`

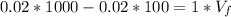
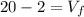
Vf = 18 m/s

Next, we would find the kinetic energy of block-bullet;

`K.E = (1)/(2)MV^(2)`

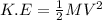
Substituting into the formula, we have;

`K.E = (1)/(2)*1*18^(2)`

`K.E = (1)/(2)*324`

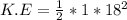
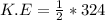
K.E = 162 Joules.

In Kilojoules;

K.E = 162/1000

K.E = 0.162 ≈ 0.16 KJ