Answer:
Part A
The estimated solution of the graph is (37/29, -30/29)
Part B
The equation of the blue line is y = 0.6·x - 1.8
The equation of the red line is y = (-4/3)·x + 2/3
Explanation:
Part A
From the given graph, we have two lines, one red and one blue line, intersecting in Quadrant IV
Given that the equation of the lines are also required, we find the solution of the graph, through the equation of the lines as follows;
The points through which the blue line passes are (-2, -3), and (3, 0)
The slope of the blue line,
 = (0 - (-3))/(3 - (-2)) = 0.6
= (0 - (-3))/(3 - (-2)) = 0.6
Therefore, we have;
y - 0 = 0.6·(x - 3)
∴ The equation of the blue line is y = 0.6·x - 1.8
The approximate points through which the red line passes are (-1, 2) and (-2.5, 4)
The slope of the red line,
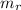 = (4 - 2)/((-2.5) - (-1)) = -4/3
= (4 - 2)/((-2.5) - (-1)) = -4/3
Therefore, we have;
y - 2 = (-4/3)·(x - (-1)) = (-4/3)·x - 4/3
∴ The equation of the red line is y = (-4/3)·x - 4/3 + 2 = (-4/3)·x + 2/3
y = (-4/3)·x + 2/3
The solution for the graph is the point where the y-values are equal
Therefore, wat the solution point, y = y, and 0.6·x - 1.8 = (-4/3)·x + 2/3
0.6·x + 4/3·x = 1.8 + 2/3
x = (1.8 + 2/3)/(0.6 + (4/3)) = 37/29 ≈ 1.28
At the solution of the graph, y = 0.6 × (37/29) - 1.8 = -30/29
Therefore, the estimated solution of the graph is (37/29, -30/29)
Part B
From the above solution of the graph, we have;
The equation of the blue line: y = 0.6·x - 1.8
The equation of the red line: y = (-4/3)·x + 2/3