Answer:
The distance to the top of the balloon is approximately 33.977 meters
Explanation:
The (horizontal) distance from the hot air balloon from the observer, l = 30 m
The angle of elevation to the top of the balloon, θ = 28°
With the balloon standing upright, the distance to the top of the balloon, d, the height of the balloon, h and the horizontal distance to the balloon, l, form a right triangle, where;
d = The hypotenuse side
l = The leg adjacent to the reference (given) angle,
h = The leg opposite to the given angle, θ
By trigonometric ratios, we have;
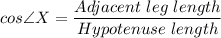
From which we get;
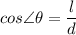
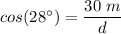
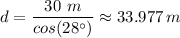
The distance to the top of the balloon, d ≈ 33.977 m