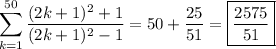It's easier to deal with the symbolic sum (in sigma notation),

Expanding the terms in the fraction, computing the quotient, and decomposing into partial fractions gives
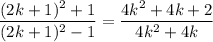
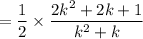

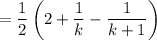
and it's the latter two terms that reveal a telescoping pattern.
In case you need more details about the partial fraction decomposition, we are looking for coefficients a and b such that
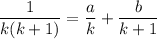
or
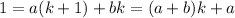
which gives a = 1, and a + b = 0 so that b = -1.
Our sum has been rearranged as
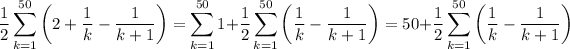
The remaining telescoping sum is
1/2 [(1/1 - 1/2) + (1/2 - 1/3) + (1/3 - 1/4) + … + (1/48 - 1/49) + (1/49 - 1/50) + (1/50 - 1/51)]
and you can see how there are pairs of numbers that cancel, so that the sum reduces to
1/2 [1/1 - 1/51] = 1/2 [1 - 1/51] = 1/2 × 50/51 = 25/51
So, our original sum ends up being