Answer: 5005
==================================================
Step-by-step explanation:
Let's say we had the slots A,B,C,D,E,F. Each slot represents where a flower would go.
For slot A, we have 15 different flowers to pick from.
Then slot B has 15-1 = 14 choices
C has 15-2 = 13 choices
and so on. We count our way down until we fill up slot F.
The count down looks like this: 15, 14, 13, 12, 11, 10
Multiply out those values: 15*14*13*12*11*10 = 3,603,600
If order mattered, then this represents the number of ways to select 6 flowers from a pool of 15 total.
However, order does not matter in this case. All that matters is the group overall.
For any group of 6 items, we have 6! = 6*5*4*3*2*1 = 720 different arrangements. That means the value 3,603,600 is too large exactly by a factor of 720.
We divide by 720 to get to (3,603,600)/720 = 5005 which is the final answer
It's the number of combinations where we select 6 from a pool of 15.
-------------------------------
As you can guess, you could use the nCr combination formula as an alternative route. Plug in n = 15 and r = 6 like so
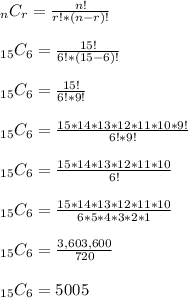
In the third to last step, notice how we have the 15*14*13*12*11*10 up top and 6*5*4*3*2*1 down below.
This value 5005 can be found in Pascal's Triangle. Look in the row that has 1, 15, ... and count out 7 spaces from the left. You should arrive at 5005. However, you'll need a fairly large Pascal's Triangle to use this method.