Answer:
A
Explanation:
The position of an atom moving inside a cathode ray tube is given by the function:
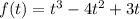
Where f(t) is in meters and t is in seconds.
And we want to determine its instantaneous velocity at t = 2.5 seconds.
The velocity function is the derivative of the position function. Thus, find the derivative of the function:
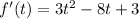
Then the instantaneous velocity at t = 2.5 will be:
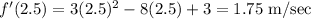
Our answer is A.