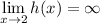Question

Function limits:
(Full development)

Answer 1

Answers:

`\displaystyle \lim_(x\to -3^(+)) h(x) = 1\\\\\displaystyle \lim_(x\to -3^(-)) h(x) = 1\\\\\displaystyle \lim_(x\to -3) h(x) = 1\\\\\displaystyle \lim_(x\to 0^(+)) h(x) = 0\\\\\displaystyle \lim_(x\to 0^(-)) h(x) = 3\\\\\displaystyle \lim_(x\to 2^(-)) h(x) = \infty\\\\\displaystyle \lim_(x\to 2^(+)) h(x) = \infty\\\\`

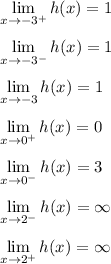
The limit exists at -3

The limit does not exist at 0

The limit exists at 2, assuming your teacher allows positive infinity to be an answer (otherwise, the limit doesn't exist).

============================================================

Step-by-step explanation:

If we start on the left side of x = -3, and approach toward x = -3 itself, then we will approach y = 1. Imagine it's like a car on a roller coaster able to move along the curve. If the car is to the left of x = -3, then it goes uphill slowly approaching that limiting value.

If we start on the right side of x = -3, and approach -3 itself, then we approach the same y value as before

So that's how I'm getting

`\displaystyle \lim_(x\to -3^(+)) h(x) = 1\\\\\displaystyle \lim_(x\to -3^(-)) h(x) = 1\\\\\displaystyle \lim_(x\to -3) h(x) = 1\\\\`

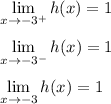
The third limit is basically the combination of the first two limits. If the LHL (left hand limit) and the RHL (right hand limit) are equal, then the limit exists.

--------------------------------------

We see that the LHL and RHL at x = 0 aren't the same. So the limit does not exist at x = 0

The LHL for x = 0 is 3 while the RHL for x = 0 is 0.

That explains why

`\displaystyle \lim_(x\to 0^(+)) h(x) = 0\\\\\displaystyle \lim_(x\to 0^(-)) h(x) = 3\\\\\\\displaystyle \lim_(x\to 0) h(x) = \text{DNE}\\\\\\`

DNE means does not exist

-------------------------------------

Lastly, when we approach x = 2 from the left, we head upward toward positive infinity.

So
`\displaystyle \lim_(x\to 2^(-)) h(x) = \infty\\\\`

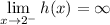
Also,
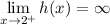`\displaystyle \lim_(x\to 2^(+)) h(x) = \infty\\\\` because we're heading upward forever when approaching x = 2 from the right side.

We can then say
`\displaystyle \lim_(x\to 2) h(x) = \infty\\\\`