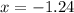Answer:
x = 3.24, x = -1.24
Explanation:
The standard form for a quadratic equation is
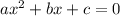 . For your equation a = 1, b = -2, c = -4. The quadratic formula you will be using is
. For your equation a = 1, b = -2, c = -4. The quadratic formula you will be using is
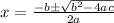 .
.
Plug in a = 1, b = -2, and c = -4 into the formula.
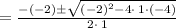
We'll do the top part first:
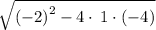
Apply rule
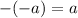
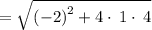
Apply exponent rule
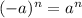 if
if
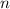 is even
is even
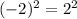
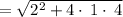
Multiply the numbers
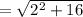
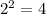
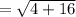
Add
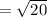
The prime factorization of 20 is
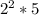
20 divides by 2. 20 = 10 * 2
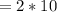
10 divides by 2. 10 = 5 * 2
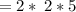
2 & 5 are prime numbers so you don't need to factor them anymore
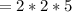
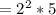
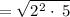
Apply radical rule
![\sqrt[n]{ab} =\sqrt[n]{a} \sqrt[n]{b}](https://img.qammunity.org/2022/formulas/mathematics/high-school/wmdv6pntulyz4nthapo63n6q5zzhbijt9x.png)
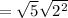
Apply radical rule
![\sqrt[n]{a^(n) } =a](https://img.qammunity.org/2022/formulas/mathematics/high-school/5llzn2003is619kpkn1wfpcig6jksbe8fy.png) ;
;
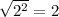
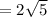
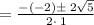
Because of the
 you have to separate the solutions so that one is positive and the other is negative.
you have to separate the solutions so that one is positive and the other is negative.
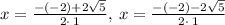
Positive x:
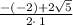
Apply rule
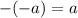
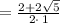
Multiply
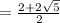
Factor
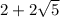 and rewrite it as
and rewrite it as
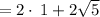 . Factor out 2 because it is the common term.
. Factor out 2 because it is the common term.
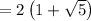 .
.
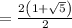
Divide 2 by 2
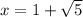 or
or
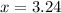 (You'll probably have to use a calculator for the square root of 5)
(You'll probably have to use a calculator for the square root of 5)
^Repeating the process of positive x for negative x in order to get
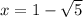 or
or