Question

Solve for x with an explanation please tha k you ok now im just trying to fill the 20 letter requirement (:

Answer 1

Given:

The given figure of a triangle.

To find:

The value of x.

Solution:

According to the angle bisector theorem, the angle bisector of a triangle divides the opposite side in two parts that are proportional to other two sides of the triangle.

Using angle bisector theorem, we get

`(2x-5)/(21)=(10)/(24-10)`

`(2x-5)/(21)=(10)/(14)`

`(2x-5)/(21)=(5)/(7)`

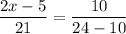
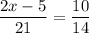
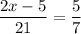
Multiply both sides by 21.

`(2x-5)/(21)* 21=(5)/(7)* 21`

`2x-5=15`

`2x=15+5`

`2x=20`

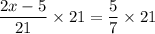
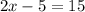
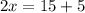
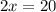
Divide both sides by 2.

`x=(20)/(2)`

`x=10`

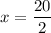
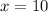
Therefore, the value of x is 10.