Question

Can anyone someone please help me:((

What is the correct standard form of the equation of the parabola?
Enter your answer below. Be sure to show each step of your work.

Answer 1

Therefore, the standard for will be:

`y=(1)/(4)x^(2)-x-4`

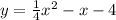
Explanation:

The equation of a parabola written as vertical axes is given by:

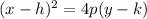`(x-h)^(2)=4p(y-k)` (1)

The vertex of the parabola (h,k) is (2,-5).

The focus (h,k+p) is (2,-4)

Then we can find p knowing that:

h = 2

k = -5

k + p = -4 then p = -4+5 = 1

Putting all these values in equation (1) we will find the equation of the parabola:

`(x-2)^(2)=4(1)(y-(-5))`

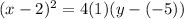
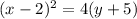`(x-2)^(2)=4(y+5)` (2)

Now, we need to find the standard form of the equation of the parabola.

Let's recall that standard form is:

`y=ax^(2)+bx+c`

We just need to work out equation (2) to convert it to the standard form.

`(x-2)^(2)=4(y+5)`

`x^(2)-4x+4=4(y+5)`

`(1)/(4)x^(2)-x+1=y+5`

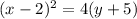
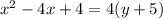
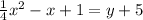
Therefore, the standard for will be:

`y=(1)/(4)x^(2)-x-4`

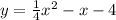
I hope it helps you!