1 Answer

Sareesh Krishnan · Answer 1 · 2022-02-08T04:24:03+0000

Given:

Number of red marbles = 5

Number of blue marbles = 4

Number of yellow marbles = 3

To find:

The probability of pulling a red marble, then pulling a blue marble, without replacement.

Solution:

Probability formula:

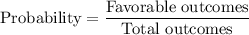
$\text{Probability}=\frac{\text{Favorable outcomes}}{\text{Total outcomes}}$

We have,

Number of red marbles = 5

Total number of marbles is:

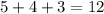
5+4+3=12

Probability of getting a red marble is:

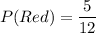
P(Red)=(5)/(12)

After selecting one red marble, the remaining number of marbles is 11 and the number of blue marbles is 3. So,

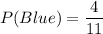
P(Blue)=(4)/(11)

Now, the probability of pulling a red marble, then pulling a blue marble, without replacement is:

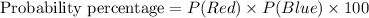
$\text{Probability percentage}=P(Red)* P(Blue)* 100$

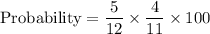
$\text{Probability}=(5)/(12)* (4)/(11)* 100$

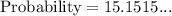
$\text{Probability}=15.1515...$

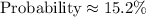
$\text{Probability}\approx 15.2\%$

Therefore, the correct option is B.

Please log in or register to add a comment.