Given:
The equation is:
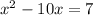
To find:
The number that should be added to sides of the equation to complete the square.
Solution:
If an expression is in the form of
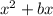 , then we have to add
, then we have to add
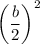 to make it perfect square.
to make it perfect square.
We have,
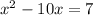 ...(i)
...(i)
To make it perfect square we need to add square of half of coefficient of x on both sides.
Coefficient of x is -10, so square of half of coefficient of x is:

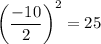
On adding 25 on both sides of (i), we get
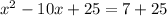
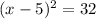
Therefore, we need to add 25 to both sides of the equation to complete the square.