The midpoint of AB is M (2,0). If the coordinates of A are, (-3, 3), what are the coordinates of B?

Question

asked May 10, 2022 77.7k views

1 Answer

Yanflea · Answer 1 · 2022-05-14T23:16:07+0000

Given:

M is the midpoint of AB.

M(2,0) and A(-3, 3).

To find:

The coordinates of point B.

Solution:

Midpoint formula:

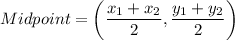
$Midpoint=\left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)$

Let the coordinates of point B are (a,b). Then, using the midpoint formula, we get

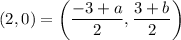
$(2,0)=\left((-3+a)/(2),(3+b)/(2)\right)$

On comparing both sides, we get

(-3+a)/(2)=2

-3+a=2* 2

a=4+3

a=7

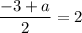
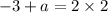
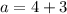
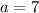
And,

(3+b)/(2)=0

3+b=0

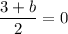
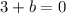
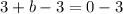
3+b-3=0-3

b=-3

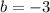
Therefore, the coordinates of point B are (7,-3).