Given:
The expression is:
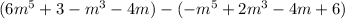
To find:
The resulting polynomial in standard form.
Solution:
We have,
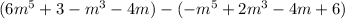
Write subtraction of a polynomial expression as addition of the additive inverse.
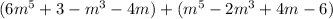
Rewrite terms that are subtracted as addition of the opposite.
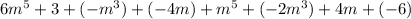
Group like terms.
![[6m^5+m^5]+[3+(-6)]+[(-m^3)+(-2m^3)]+[(-4m)+4m]](https://img.qammunity.org/2022/formulas/mathematics/high-school/lquj7dqmj7naw29olkv3zlfv9oa4pdqdx4.png)
Combine like terms.
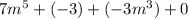
On simplification, we get

Write the polynomial in standard form.
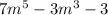
Therefore, the required polynomial in standard form is
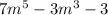 .
.