Answer:
1.
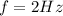
2.

3.
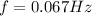
4.
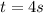
Step-by-step explanation:
1. The frequency of rotation is given by:
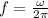
Where:
ω: is the angular speed = 50 rotations (revolutions) in 25 s.
We need to convert the units of ω.
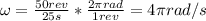
Now, the frequency is:
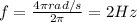
2. The frequency is:
We know:
5 laps = 5 revolutions
t: time = 450 s
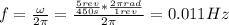
3. The frequency of the pendulum is:
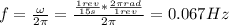
4. We have:
θ: number of revolutions = 48 rev
f = 12 Hz
t =?
The time can be calculated as follows:
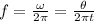
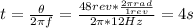
I hope it helps you!