Answer:
![\mathbf{ (\pi)/(675)\Big[ 34√(34) -125\Big] }](https://img.qammunity.org/2022/formulas/mathematics/college/jwngagsaxxuh7a3nm6s8uv7z3yvfmyj9uq.png)
Explanation:
The curve x = f(y)
The area of the surface around the y-axis from y = a → y = b is:
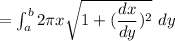
From the given curve:
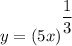 ; assuming the region bounded by the curve is 0 ≤ y ≤ 1
; assuming the region bounded by the curve is 0 ≤ y ≤ 1
So;
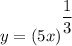
5x = y³
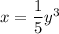
The differential of the above equation Is:
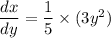
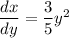
Now, we have the area of the surface produced around the curve
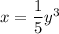 through the y axis from the region y = 0 to y = 1
through the y axis from the region y = 0 to y = 1
∴
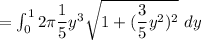
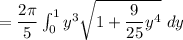
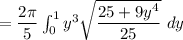
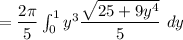
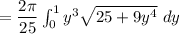
Let make
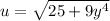
It implies that:
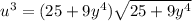
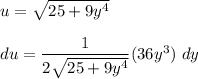
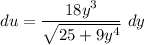
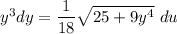
when y = 0 ;
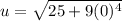
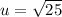
u = 5
when y = 1;
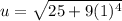
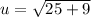
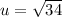
∴
The equation
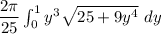 can be written as:
can be written as:
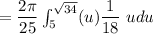
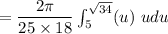
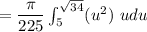
![= (\pi)/(225)\Big[ (u^3)/(3) \Big] ^(√(34))_(3)\\](https://img.qammunity.org/2022/formulas/mathematics/college/ly3k2y9ar0jno2sza3g3fsttxzvhkf518k.png)
![\mathbf{= (\pi)/(675)\Big[ 34√(34) -125\Big] }](https://img.qammunity.org/2022/formulas/mathematics/college/7okhqz1e91zlf5hdo43geyrdfwt5yjy77x.png)