Question

A child on a tricycle is moving at a speed of 1.40 m/s at the start of a 2.25 m high and 12.4 m long incline. The total mass is 48.0 kg, air resistance and rolling resistance can be modeled as a constant friction force of 41.0 N, and the speed at the lower end of the incline is 6.50 m/s. Determine the work done (in J) by the child as the tricycle travels down the incline.

Answer 1

The work done by the child as the tricycle travels down the incline is 416.96 J

Step-by-step explanation:

Given;

initial velocity of the child,
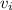`v_i` = 1.4 m/s

final velocity of the child,
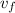`v_f` = 6.5 m/s

initial height of the inclined plane, h = 2.25 m

length of the inclined plane, L = 12.4 m

total mass, m = 48 kg

frictional force,
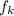`f_k` = 41 N

The work done by the child is calculated as;

`\Delta E_(mech) = W - f_(k) \Delta L\\\\W = \Delta E_(mech) + f_(k) \Delta L\\\\W = (K.E_f - K.E_i) + (P.E_f - P.E_i) + f_(k) \Delta L\\\\W = (1)/(2) m(v_f^2 - v_i^2) + mg(h_f - h_i) + f_(k) \Delta L\\\\W = (1)/(2) * 48(6.5^2 - 1.4^2) + 48* 9.8(0-2.25) + (41* 12.4)\\\\W = 966.96 \ - \ 1058.4 \ + \ 508.4\\\\W = 416.96 \ J`

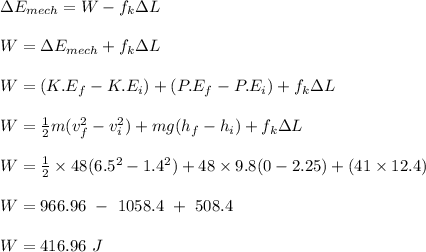
Therefore, the work done by the child as the tricycle travels down the incline is 416.96 J